¿QUÉ ES UN INTERVALO?
Un
intervalo es la diferencia de altura entre dos sonidos. Esta
definición incluye tanto a los sonidos que suenan
simultáneamente (ej: acordes) como a los que lo hacen de
forma sucesiva (melodías, etc…).
Ejemplos de intervalos
(sucesivo, simultáneo)
DISTANCIAS: TONO Y SEMITONO
Las distancias normales entre dos notas, son dos: tono y semitono.
Distribución de tonos y semitonos en el teclado del piano.
Existen dos tipos de semitonos:
Semitono cromático: Las dos notas que forman el intervalo de semitono tienen el mismo nombre.
Ejemplo de Semitono cromático.
Semitono diatónico: Las dos notas que forman el
intervalo de semitono tienen nombres
distintos.
Ejemplo de Semitono diatónico.
Suenan igual porque la diferencia entre semitono diatónico
y cromático no es sonora, sino de escritura. la distancia es la
misma (1 semitono entre Do y Do#, 1 semitono entre Do y Reb).
TONO
1 Tono =
2 Semitonos.
Si
tomamos como base las notas naturales (que forman la escala de Do Mayor) las distancias
entre las notas son las siguientes:
Distribución de tonos y semitonos (notas naturales) en el teclado
del piano.
La distancia entre las notas Do y Re es de un tono, mientras que
entre Mi y Fa tan solo hay un semitono de diferencia. Las notas están separadas por semitonos,
significa que entre las notas Do y Re se sitúa una nota intermedia.
En el piano se ve claramente, las teclas negras que se sitúan en la parte superior del teclado, entre dos teclas adyacentes. Cada nota que está separada por un tono de la siguiente, tiene una tecla negra situada entre las dos.
NUMERACION DE UN INTERVALO.
La numeración de un intervalo se realiza contando el numero de notas que abarca incluyendo las notas que forman dicho intervalo.
En el ejemplo anterior observamos cómo en el intervalo SOL-MI hay 6 notas de distancia, luego el intervalo será de 6ª. (por ejemplo: entre Do y Sol hay una quinta o 5ª, entre Re y Fa una tercera o 3ª, etc…).
Estas
notas pueden estar o no alteradas. Como las notas de las que partimos para numerar el intervalo pueden estar
alteradas, realmente con el número no sabemos exactamente el número de tonos y
semitonos que existe entre el intervalo.
Ejemplo de
intervalo de terceras.
Por
ejemplo, entre Do y Mi existe una 3ª y la distancia es de 2 tonos, mientras que
entre Do y Mi bemol también existiría una 3ª y sin embargo el intervalo real
sería de 1 tono y 1 semitono.
Por lo
tanto, necesitamos calificar los intervalos de alguna forma que nos permita
distinguir unívocamente un intervalo del resto.
Para
completar la numeración se añade un calificativo de dicho intervalo, que puede
ser: Mayor, Menor, Justo, Aumentado o Disminuido.
Primera
aclaración: Los calificativos “mayor” y “menor” tan sólo se emplean en segundas
(2ª), terceras (3ª), sextas (6ª) y séptimas (7ª), mientras que el calificativo
“justo” tan sólo puede ser empleado en cuartas (4ª), quintas (5ª) y octavas
(8ª).
Intervalos Mayores -M-, Menores -m- y Justos -J-
Escala de Do natural (intervalos mayores y justos)
·
2ª Mayor = 1 Tono
·
3ª Mayor = 2 Tonos
·
4ª Justa = 2 Tonos + 1 Semitono
·
5ª Justa = 3 Tonos + 1 Semitono
·
6ª Mayor = 4 Tonos + 1 Semitono
·
7ª Mayor = 5 Tonos + 1 Semitono
·
8ª Justa = 6 Tonos
Si
tomamos las notas naturales desde MI obtenemos los intervalos menores y justos:
Escala de Mi natural (intervalos menores y justos).
·
2ª menor = 1 Semitono
·
3ª menor = 1 Tono + 1 Semitono
·
4ª Justa = 2 Tonos + 1 Semitono (igual que desde Do)
·
5ª Justa = 3 Tonos + 1 Semitono (igual que desde Do)
·
6ª menor = 4 Tonos
·
7ª menor = 5 Tonos
·
8ª Justa = 6 Tonos (igual que desde Do)
INTERVALOS AUMENTADOS Y DISMINUIDOS.
Los calificativos “aumentado” y “disminuido”, se pueden emplear
en cualquier intervalo, de la siguiente forma:
·
Los intervalos aumentados tienen un semitono más que su
respectivo intervalo Mayor (o Justo).
Ejemplos de Intervalos aumentados.
Se puede
conseguir un intervalo aumentado a partir de uno justo (o mayor) de dos formas:
aumentando en un semitono la nota superior (como en el primer ejemplo) o disminuyendo
la nota inferior en un semitono (como en el segundo ejemplo, convirtiendo el Mi
en Mi bemol). Con las dos opciones conseguimos que el intervalo se amplíe un
semitono.
·
Los intervalos disminuidos tienen un semitono menos que su
respectivo intervalo Menor (o Justo).
Ejemplos de Intervalos disminuidos.
Para
crear un intervalo disminuido a partir de uno menor (o justo) debemos reducir
el intervalo en un semitono. Como hemos visto, se podría hacer reduciendo en un
semitono la nota superior (Sol -> Sol bemol) o aumentando en un semitono la
nota inferior (Fa -> Fa #).
TABLA DE INTERVALOS
Ya hemos
visto cómo podemos nombrar cualquier intervalo (que esté dentro de una octava).
podemos ver que todos los intervalos menores tienen un semitono menos que
sus respectivos mayores (por ejemplo, una 3ª Mayor tiene 2 Tonos mientras que
una 3ª menor tiene 1 tono y 1 semitono).
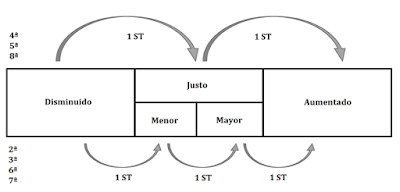
Por
tanto, el esquema que se sigue para calificar un intervalo es el siguiente:
Esquema de
calificación de un intervalo.
Si
calculamos las distancias que existen (en tonos y semitonos) para cada tipo de
intervalo (ya numerado y calificado) obtendremos una tabla como ésta (que
resume todo lo explicado anteriormente):
Tabla general
de intervalos (ejemplo desde la nota DO)
En esta
tabla se resumen las distancias que existen desde la nota DO hasta cualquier
otra (dentro del ámbito de una 8ª).
CASOS ESPECIALES
Unísono: Se denomina unísono a dos notas de igual nombre y sonido. El unísono en sí no constituye un intervalo, ya que no existe distancia entre las notas.
Enarmonía: Una enarmonía se produce entre dos notas que tienen el mismo sonido y escritura diferente. Puesto que no existe distancia entre dos notas enarmónicas, no se considera un intervalo.
Ejemplo de notas enarmónicas.
2ª disminuida
Una
segunda disminuida no constituye un intervalo, ya que
no existe distancia entre las notas. Se corresponde, por tanto, con
una enarmonía.
Ejemplo de segundas disminuidas.
TIPOS DE INTERVALO
INTERVALOS ASCENDENTES Y DESCENDENTES
Los
intervalos ascendentes se producen entre dos sonidos sucesivos, cuando el
segundo es más agudo que el primero.
Ejemplos de Intervalos ascendentes.
Un
intervalo es conjunto si sus sonidos (con o sin alteraciones) ocupan grados inmediatos
(Sol-La, Si-Do, Fa-Mi, ,etc..). Es decir, cuando son intervalos de segunda.
Ejemplo de Intervalos conjuntos.
Son disjuntos cuando no se sigue el orden sucesivo (existe un “salto”). Aquí se encuentran los intervalos de 3ª, 4ª, 5ª, etc…
Ejemplo de Intervalos disjuntos
Los
intervalos melódicos se dan entre dos sonidos
sucesivos (uno después de otro, como en una melodía).
Ejemplo de Intervalos armónicos.
Los
intervalos simples son aquellos que se sitúan dentro
del ámbito de una octava justa (8ª J).
¿Qué
intervalo simple es el asociado de uno compuesto?
Para
saberlo, debemos reducir la distancia (eliminando octavas) hasta que la
extensión del intervalo quede dentro del ámbito de una 8ª. Esto puede
realizarse bien subiendo la nota inferior de octava en octava, bien
descendiendo la nota superior.
Por
ejemplo, el intervalo simple que se corresponde con un intervalo de 10ª m sería
una 3ª m:
Ejemplo de Intervalo compuesto y simple asociado.
Escucha
los siguientes intervalos:
Ahora
escucha estos otros:
Ejemplo de Consonancia imperfecta.
Lo normal es que también suenen agradables, aunque algo menos «claros» que los anteriores.
Entre estos intervalos se produce una consonancia
imperfecta.
Estos
intervalos puede resultar más chocantes:
Por
último, existen 2 intervalos que tienen una sensación auditiva algo imprecisa
(ni consonancia ni disonancia). Son la 4ª aumentada y su inversión, la 5ª
disminuida. Ambos intervalos tienen la misma extensión (3 tonos, o intervalo de tritono Do-Fa# y
Do-Solb, por ejemplo). Entre estos intervalos se produce lo que se denomina
una semiconsonancia.
Invertir
un intervalo es convertir la nota inferior en la superior, y viceversa (la nota
superior pasa a ser la nota inferior).
¿Cómo se
realiza la inversión?
Elevando
una 8ª la nota inferior del intervalo, o disminuyendo una 8ª la nota superior.
De esta forma, un intervalo como Do-Mi pasaría a ser Mi-Do, por ejemplo.
Ejemplo de Inversión de un intervalo.
Un intervalo y su inversión siempre suman numéricamente una 9ª. Quiere decir que una 2ª se convertirá en una 7ª, una 3ª en una 6ª, una 4ª en una 5ª, una 5ª en una 4ª, etc… La inversión de una 8ª sería el unísono.
La calificación de un intervalo y su inversión son: m -> M (si un intervalo es menor, su inversión es mayor), M->m, J->J, aum-> dism, dism-> aum.
Calificación
de un intervalo (normal e inversión).
Algunos ejemplos de intervalos invertidos:
Esquema de inversión de intervalos
·
3ª M -> 6ª m (3+6=9, M->m)
·
4ª J -> 5ª J (4+5=9, J->J)
·
2ª aum -> 7ª dism (2+7=9, aum->dism)
RECAPITULACION ESPECIES DE INTERVALOS






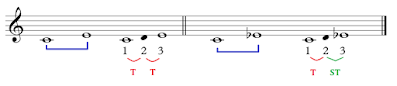

















































No hay comentarios.:
Publicar un comentario